The Impact of Colleges on Home Prices in US Cities

Summary: Comparing changes in single family home sale prices since 1996 amongst U.S. cities with fewer than 250,000 residents reveals that cities with universities—or college towns—see higher increases in sale prices than do non-college towns. College towns outperform non-college towns in month-to-month changes in average home sale prices (higher increases and lower decreases) 56% of the time. This, over time, compounds as college towns seeing a 130.33% increase in home sale prices compared to 82.16% for non-college towns over the last 25 years.

Introduction

Preliminary data exploration indicates that in the years since 1996, college towns have seen a higher average increase in both single-family home sale prices, as well as in population, than have like-sized cities without colleges. Is the presence of a college or university a factor in this? Or is population size a stronger predictor of home sale prices? (College towns tend to have slightly higher population sizes than non-college towns) Or is this difference just an illusion created by the effects of compound returns based on an initially smaller price difference?

Throughout this study, a college town is defined as a city in the United States which is home to at least one college or university and which had a population of fewer than 250,000 people in 2010. 2010 is used as the base year for the population metric, as it is the date of the last published full U.S. census, in addition to being approximately in the middle of the date range of available home sale price data. 250,000 is the cut-off because this is the approximate lower limit for population size such that 95% of U.S. cities with colleges meet the proposed definition.

This study examines the question of whether homes in college towns are better financial investments than homes in non-college towns, measured by percentage increases in home sale values. It finds that, although this has been the case in the past, a city’s status as a college town is not a strong enough indicator of higher return rates to predict that these rates will remain higher in the future.

This finding is based on the consideration of the following questions:

In years when the average sale price of single-family homes rises, do college towns see a higher increase in home sale prices from the previous year than do non-college towns?
In years when the average sale price of single-family homes falls, do college towns see a lower decrease in home sale prices from the previous year than do non-college towns?
Is the presence of a college town a stronger predictor of a higher increase in home values than is its population size?
Are the above values consistent in the months since March 2020 with those since 1996?

Findings indicate that homes in college towns have been a better, more secure investment—they yield higher returns on investment in good years and reduce risk in down years. The difference in single-family home sale price performance between college towns and non-college towns is slight, independent of population size, and over time, compounds into a significant home value discrepancy. Potentially due to limitations in the data, however, it is difficult to prove statistical significance for these differences.

Data description

Why this dataset was created

The dataset used in this study was created to facilitate examining the effect of a college or university in small to mid-sized U.S. cities. It merges publicly available datasets as well as information publicly available on the web.

Dataset sources

The dataset used in this study is the product of combining three data sources:

1. Zillow house sale prices

Zillow provides time-series data on house sale prices for towns and cities in the United States (https://www.zillow.com/research/data/). This study is using their "ZHVI Single Family Homes Time Series($)" Dataset for U.S. Cities. Zillow makes this data publicly available in the hopes that users will create better home-value predictive models, so there is a financial motivation to its distribution. Because this particular dataset averages sale prices of single-family homes at a city level, no personal information is being made public. Zillow does, however, distribute datasets at both coarser and finer-grained levels of detail. These range from state-level to neighborhood-level. At a neighborhood level, a degree of personal information is inferable about individuals. Given that there is access to an individual's address from another source, one could infer wealth (or home-debt). How Zillow collects data is not detailed. Individuals whose data are shared are likely not informed that this information is being made public.

2. United States Census population data

The United States Census provides time-series data for populations of Incorporated Places in the United States from 2010 to 2019 (https://www.census.gov/data/tables/time-series/demo/popest/2010s-total-cities-and-towns.html). The Census Bureau collects and publishes this data as is required by the United States constitution. Individuals counted in the census are aware that this data is being made publicly available and are legally required to provide it. No personally identifiable information is shared.

3. College towns in the United States

Data scraped from https://en.wikipedia.org/wiki/List_of_college_towns has been filtered to include only cities in the United States. This data is publicly created, edited, and distributed under the Creative Commons Attribution-ShareAlike License.

Dataset description

The resulting dataset used in this study contains 310 columns and 16,885 rows. The columns contain information on the following variables:

city: The city's name
city_state: The city's state (abbreviation)
colleges_count: The number of colleges/universities in the city
pop_2010 through pop_2019: The population of the city each year between 2010 and 2019 inclusive
1996-01-31 through 2021-04-30: The average sale price of single-family homes in that city for each month between January 1996 and May 2021

Each row represents a city in the United States with a population of less than 250,000 in 2010. Each observation contains the city, state, college count, and population data. The level of completeness for home sale price data varies, however, especially in the earlier years in the date range.

Privacy concerns

Although no personally identifiable information exists in this dataset, it does, with a broad brush, potentially imply financial information about homeowners in various cities.

Data processing

The number of observations available in this study is smaller than that of the original datasets. This study only includes cities included in the census population dataset (which is smaller than the Zillow home sale price dataset). Of those cities, only those with populations smaller than 250,000 are included. Finally, from that, a handful of observations were removed because the identifiers between datasets (city names and states) didn't match and weren't reliably manually correctable.

For complete information on data sources, cleanup, and sample size selection, see Appendix - Datasets: Sources and cleanup.

Raw data

Raw datasets are available via the following links:

The dataset used in this study is available here:

Final Dataset (29.2 MB)

Preregistration statement

Intuitively, one might assume that homes in college towns should be a stable financial investment. A college is a stable source of employment for a city, it provides a regular influx of capital from visiting students that supports the local economy, and it drives high demand for rental properties, which, in turn, increases home values.

2020 has seen a shift in many facets of the economy due to COVID-19. Many colleges are offering either partial or completely online options; with that, fewer students are moving to college towns for the school year. Will this have an impact on housing prices? Or are housing prices valued within a longer-term framework so that this temporary change in the economy won't reflect significantly different trends in housing sale prices in college towns relative to non-college towns?

This study aims to prove the following hypotheses:

College towns are better investments than non-college towns based on returns on home sale prices. In years when the average sale price of single-family homes rises, college towns see a higher increase in home sale prices from the previous year than do non-college towns. And in years when the average sale price of single-family homes falls, college towns see a lower decrease in home sale prices from the previous year than do non-college towns.
The investment security of college towns is consistent in the months since March 2020 to the present, with those since 1996.
The presence of a college town is a stronger predictor of a higher increase in home values than is population size (in cities with populations smaller than 250,000).

Evaluating the data

## load libraries
import pandas as pd
import numpy as np

## For Visualizing
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from matplotlib.dates import DateFormatter

# for analysis
from sklearn.linear_model import LinearRegression
from scipy import stats
from scipy.stats import ttest_ind

# Import dataset
# data = pd.read_csv("working_dataset.csv")
data = pd.read_csv("working_dataset-2021-06-05.csv")

dataA = data.loc[(data.colleges_count == 0)]['pop_2010']
dataB = data.loc[(data.colleges_count > 0)]['pop_2010']

plt.ylabel('Population')
plt.title('Distribution of cities with populations < 250,000 in 2010')
plt.boxplot( [ dataA, dataB ], showfliers=True, labels=[ 'Non-College Towns', 'College Towns' ])
plt.show()

data_ct = data.loc[(data.colleges_count > 0)]
data_nct = data.loc[(data.colleges_count == 0)]
print( "Non-college town population mean (cities < 250,000): {:.2f}".format( data_nct['pop_2010'].mean()) ) 
print( "College town population mean (cities < 250,000): {:.2f}".format( data_ct['pop_2010'].mean()) ) 
print( "Non-college town population standard deviation (cities < 250,000): {:.2f}".format( data_nct['pop_2010'].std()) ) 
print( "College town population standard deviation (cities < 250,000): {:.2f}".format( data_ct['pop_2010'].std()) )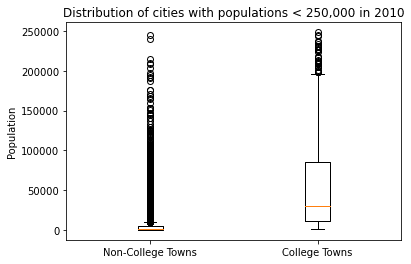

Non-college town population mean (cities < 250,000): 5936.40
College town population mean (cities < 250,000): 55660.60
Non-college town population standard deviation (cities < 250,000): 14699.97
College town population standard deviation (cities < 250,000): 59501.94

Comparing the distribution of population sizes in college and non-college towns

Of cities whose populations were less than 250,000 in 2010, those with colleges are, on average, significantly larger (55,660.60 population mean compared to 5,936.40). The standard deviation of population size is also higher (59,501.94 std compared to 14,699.97). This large discrepancy in the distribution between the two sets highlights the necessity of separating the effects of colleges from the effects of population size on home-sale price changes.

index = data.loc[:,'pop_2010':'pop_2019'].columns.tolist()
columns = ['nct_pop', 'ct_pop']
array = np.zeros( ( len(index), len(columns) ), dtype=float )
compare_mean_pop = pd.DataFrame(array, columns=columns, index=index)

for column in data.loc[:,'pop_2010':'pop_2019'].columns.tolist():
    compare_mean_pop['nct_pop'][column] = data[column].loc[ (data[column] > 0) & (data['colleges_count'] == 0) ].mean()

for column in data.loc[:,'pop_2010':'pop_2019'].columns.tolist():
    compare_mean_pop['ct_pop'][column] = data[column].loc[ (data[column] > 0) & (data['colleges_count'] > 0) ].mean()
    
fig = plt.figure()
plt.plot(index, compare_mean_pop.nct_pop, label="Non-College Towns")
plt.plot(index, compare_mean_pop.ct_pop, label="College Towns")
plt.title('Population mean of US cities smaller than 250,000')
plt.xlabel('Year')
plt.xticks(["pop_2010", "pop_2011", "pop_2012", "pop_2013", "pop_2014", "pop_2015", "pop_2016", "pop_2017", "pop_2018", "pop_2019"],
          ["2010", "2011", "2012", "2013", "2014", "2015", "2016", "2017", "2018", "2019"])
plt.ylabel('Population Mean')
plt.ylim(bottom=0)
plt.legend()
plt.show()

nct_mean_2010 = compare_mean_pop['nct_pop']['pop_2010']
nct_mean_2019 = compare_mean_pop['nct_pop']['pop_2019']
ct_mean_2010 = compare_mean_pop['ct_pop']['pop_2010']
ct_mean_2019 = compare_mean_pop['ct_pop']['pop_2019']
print("College town populatio mean 2010: {:.2f}".format( ct_mean_2010 ))
print("Non-college town populatio mean 2010: {:.2f}".format( nct_mean_2010 ))
print("College town populatio mean 2019: {:.2f}".format( ct_mean_2019 ))
print("Non-college town populatio mean 2019: {:.2f}".format( nct_mean_2019 ))
print("Percentage growth in population of college towns from 2010–2019: {:.2f}%".format( (ct_mean_2019 - ct_mean_2010) / ct_mean_2010 * 100))
print("Percentage growth in population of non-college towns from 2010–2019: {:.2f}%".format( (nct_mean_2019 - nct_mean_2010) / nct_mean_2010 * 100))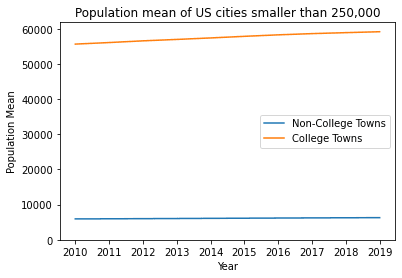

College town populatio mean 2010: 55660.60
Non-college town populatio mean 2010: 5936.40
College town populatio mean 2019: 59184.06
Non-college town populatio mean 2019: 6301.94
Percentage growth in population of college towns from 2010–2019: 6.33%
Percentage growth in population of non-college towns from 2010–2019: 6.16%

Population growth of college towns and non-college towns between 2010 and 2019

In 2010, the mean population size of college towns was 55,660.60 compared to 5,936.40 for non-college towns. By 2019, the population means had increased to 59,184.06 and 6,301.94, respectively. This increase, however, represents a population growth of relatively the same percentage for both groups—6.33% for college towns and 6.16% for non-college towns over that period.

index = data.loc[:,'1996-01-31':'2021-04-30'].columns.tolist()
columns = ['nct_price', 'ct_price']
array = np.zeros( ( len(index), len(columns) ), dtype=float )
compare_price = pd.DataFrame(array, columns=columns, index=index)

for column in data.loc[:,'1996-01-31':'2021-04-30'].columns.tolist():
    compare_price['nct_price'][column] = data[column].loc[ (data[column] > 0) & (data['colleges_count'] == 0) ].mean()

for column in data.loc[:,'1996-01-31':'2021-04-30'].columns.tolist():
    compare_price['ct_price'][column] = data[column].loc[ (data[column] > 0) & (data['colleges_count'] > 0) ].mean()
    
plt.title('Sale price of Singel Family Homes (SFH) in US cities smaller than 250,000')
plt.ylabel('SFH mean sale price')
plt.xlabel('Year')
plt.plot(index, compare_price.nct_price, label="Non-college Towns")
plt.plot(index, compare_price.ct_price, label="College Towns")
plt.xticks(['1996-01-31','2000-01-31','2005-01-31','2010-01-31','2015-01-31','2020-01-31'],
           ['1996', '2000', '2005', '2010', '2015', '2020'])
plt.ylim(bottom=0)
plt.legend()
plt.show()


nct_price_1996 = compare_price['nct_price']['1996-01-31']
nct_price_2021 = compare_price['nct_price']['2021-04-30']
ct_price_1996 = compare_price['ct_price']['1996-01-31']
ct_price_2021 = compare_price['ct_price']['2021-04-30']

print("College town single-family home sale price mean, 1996: ${:.2f}".format(ct_price_1996) )
print("Non-college town single-family home sale price mean, 1996: ${:.2f}".format(nct_price_1996) )
print("College town single-family home sale price mean, 2021: ${:.2f}".format(ct_price_2021) )
print("Non-college town single-family home sale price mean, 2021: ${:.2f}".format(nct_price_2021) )
print("Percentage increase in sale values in college towns from 1996–2021: {:.2f}%".format( (ct_price_2021 - ct_price_1996) / ct_price_1996 * 100 ) )
print("Percentage increase in sale values in non-college towns from 1996–2021: {:.2f}%".format( (nct_price_2021 - nct_price_1996) / nct_price_1996 * 100 ) )

College town single-family home sale price mean, 1996: $124118.75
Non-college town single-family home sale price mean, 1996: $117762.55
College town single-family home sale price mean, 2021: $285883.85
Non-college town single-family home sale price mean, 2021: $214516.54
Percentage increase in sale values in college towns from 1996–2021: 130.33%
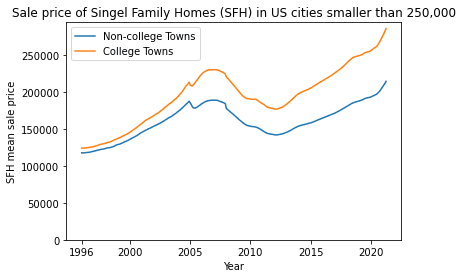
Percentage increase in sale values in non-college towns from 1996–2021: 82.16%

Average sale price of single-family homes between 1996 and 2021 for college and non-college towns

In January 1996, the average sale price of a single-family home in college towns was $124,118.75, compared with $117,762.55 in non-college towns. By January 2021, the average sale prices had increased to $285,883.85 and $214,516.54, respectively. College towns saw an increase in home sale prices over this twenty-four year period of $161,765.1, whereas non-college towns only saw an increase of $96,753.99. This growth represents a 130.33% increase for college towns compared to only a 82.16% increase for their non-college town counterparts.

# Monthly changes in home sale values, and comparing difference between CT and NCT
months = data.loc[:,'1996-01-31':'2021-04-30'].columns.tolist()
index = months[1:]
columns = ['nct_mean', 'ct_mean', 'nct_diff', 'ct_diff', 'nct_prcnt', 'ct_prcnt', 'all_mean', 'all_diff']
array = np.zeros( ( len(index), len(columns) ), dtype=float )
monthly_data = pd.DataFrame(array, columns=columns, index=index)

for month, i in zip(months, range(0, len(months)) ):
    # for each month after the first
    if i>0:
        # non-college town
        nct_prev_month = data[prev].loc[ (data[prev] > 0) & (data['colleges_count'] == 0) ].mean()
        nct_this_month = data[month].loc[ (data[month] > 0) & (data['colleges_count'] == 0) ].mean()
        nct_change = nct_this_month - nct_prev_month
        monthly_data.loc[month, 'nct_mean'] = nct_this_month
        monthly_data.loc[month, 'nct_diff'] = nct_change
        monthly_data.loc[month, 'nct_prcnt'] = nct_change / nct_prev_month * 100
        
        # college town
        ct_prev_month = data[prev].loc[ (data[prev] > 0) & (data['colleges_count'] > 0) ].mean()
        ct_this_month = data[month].loc[ (data[month] > 0) & (data['colleges_count'] > 0) ].mean()
        ct_change = ct_this_month - ct_prev_month
        monthly_data.loc[month, 'ct_mean'] = ct_this_month
        monthly_data.loc[month, 'ct_diff'] = ct_change
        monthly_data.loc[month, 'ct_prcnt'] = ct_change / ct_prev_month * 100
        
        # all cities
        all_prev_month = data[prev].loc[ (data[prev] > 0) ].mean()
        all_this_month = data[month].loc[ (data[month] > 0) ].mean()
        all_change = all_this_month - all_prev_month
        monthly_data.loc[month, 'all_mean'] = all_this_month
        monthly_data.loc[month, 'all_diff'] = all_change
    prev = month

monthly_data = monthly_data.reset_index()
monthly_data.rename(columns = {'index':'date'}, inplace = True) 
monthly_data['date'] = pd.to_datetime(monthly_data['date'], format="%Y-%m-%d")


# Monthly changes in home sale values, and comparing difference between CT and NCT
years = []
for i in range(1997, 2021):
    years.append(i)
index = years
columns =  ['nct_mean', 'ct_mean', 'nct_diff', 'ct_diff', 'nct_prcnt', 'ct_prcnt', 'all_mean', 'all_diff']
array = np.zeros( ( len(index), len(columns) ), dtype=float )
yearly_data = pd.DataFrame(array, columns=columns, index=index)
januaries = ['1996-01-31', '1997-01-31','1998-01-31', '1999-01-31', '2000-01-31', '2001-01-31', '2002-01-31', '2003-01-31', '2004-01-31', '2005-01-31', '2006-01-31', '2007-01-31', '2008-01-31', '2009-01-31', '2010-01-31', '2011-01-31', '2012-01-31', '2013-01-31', '2014-01-31', '2015-01-31', '2016-01-31', '2017-01-31', '2018-01-31', '2019-01-31', '2020-01-31', '2021-01-31']

for year, i in zip(years, range(0, len(years)) ):
    nct_current_year = data[januaries[i]].loc[ (data[januaries[i]] > 0) & (data['colleges_count'] == 0) ].mean()
    ct_current_year = data[januaries[i]].loc[ (data[januaries[i]] > 0) & (data['colleges_count'] > 0) ].mean()
    all_current_year = data[januaries[i]].loc[ (data[januaries[i]] > 0) ].mean()
    if i>0:
        nct_prev_year = data[januaries[i-1]].loc[ (data[januaries[i-1]] > 0) & (data['colleges_count'] == 0) ].mean() 
        nct_change = nct_current_year - nct_prev_year
        yearly_data.loc[year, 'nct_diff'] = nct_change
        yearly_data.loc[year, 'nct_prcnt'] = nct_change / nct_prev_year * 100
        ct_prev_year = data[januaries[i-1]].loc[ (data[januaries[i-1]] > 0) & (data['colleges_count'] > 0) ].mean() 
        ct_change = ct_current_year - ct_prev_year
        yearly_data.loc[year, 'ct_diff'] = ct_change
        yearly_data.loc[year, 'ct_prcnt'] = ct_change / ct_prev_year * 100
        all_prev_year = data[januaries[i-1]].loc[ (data[januaries[i-1]] > 0) ].mean() 
        all_change = all_current_year - all_prev_year
        yearly_data.loc[year, 'all_diff'] = all_change
    yearly_data.loc[year, 'nct_mean'] = nct_current_year
    yearly_data.loc[year, 'ct_mean'] = ct_current_year
    yearly_data.loc[year, 'all_mean'] = all_current_year

yearly_data = yearly_data.reset_index()
yearly_data.rename(columns = {'index':'date'}, inplace = True) 
yearly_data['date'] = pd.to_datetime(yearly_data['date'], format="%Y")

# Summary stats
print( "difference between CT and non-CT ($ mean): {:.2f}".format( (monthly_data['ct_diff'] - monthly_data['nct_diff']).mean() ) )
print( "difference between CT and non-CT (% mean): {:.2f}".format( (monthly_data['ct_prcnt'] - monthly_data['nct_prcnt']).mean() ) )
print( "Standard deviation in monthly return percent: {:.2f}".format( (monthly_data['ct_prcnt'] - monthly_data['nct_prcnt']).std() ))
print( "Number of months observed: {}".format(monthly_data['date'].count()) )
print( "Number of months college towns performed better (higher positive or lower negative returns): {}".format(monthly_data.loc[ (monthly_data['ct_diff'] > monthly_data['nct_diff']) ]['date'].count()) )

month_positive = monthly_data.loc[ monthly_data['all_diff'] > 0]
print( "Number of months housing prices went up: {}".format(month_positive['date'].count() ) )
print( "In positive return months, the difference between CT and non-CT ($ mean): {:.2f}".format( (month_positive['ct_diff'] - month_positive['nct_diff']).mean() ) )
print( "In positive return months, the difference between CT and non-CT (% mean): {:.2f}".format( (month_positive['ct_prcnt'] - month_positive['nct_prcnt']).mean() ) )
print( "Standard deviation in return percent in positive months: {:.2f}".format( (month_positive['ct_prcnt'] - month_positive['nct_prcnt']).std() ) )

month_negative = monthly_data.loc[ monthly_data['all_diff'] < 0]
print( "Number of months housing prices went down: {}".format(month_negative['date'].count() ) )
print( "In negative return months, the difference between CT and non-CT ($ mean): {:.2f}".format( (month_negative['ct_diff'] - month_negative['nct_diff']).mean() ))
print( "In negative return months, the difference between CT and non-CT (% mean): {:.2f}".format( (month_negative['ct_prcnt'] - month_negative['nct_prcnt']).mean() ))
print( "Standard deviation in return percent in negatie months: {:.2f}".format( (month_negative['ct_diff'] - month_negative['nct_diff']).std() ) )
print( "\n")

yearly_diff_mean = (yearly_data['ct_diff'] - yearly_data['nct_diff']).mean()
yearly_diff_percent = (yearly_data['ct_prcnt'] - yearly_data['nct_prcnt']).mean()
# print( "Difference in yearly sale price mean changes (positive = CT higher): {:.2f}".format(yearly_diff_mean) )
# print( "Difference in yearly sale price mean changes as percentage (positive = CT higher): {:.4f}".format(yearly_diff_percent) )
print("Number of years observed: {}".format(yearly_data['date'].count()) )
print("Number of years college towns performed better (higher positive or lower negative returns): {}".format(yearly_data.loc[ (yearly_data['ct_diff'] > yearly_data['nct_diff']) ]['date'].count()) )

yearly_positive = yearly_data.loc[ yearly_data['all_diff'] > 0]
print("number of years housing prices went up: {}".format(yearly_positive['date'].count() ) )
print("In positive return years, the difference between CT and non-CT ($ mean): {:.2f}".format( (yearly_positive['ct_diff'] - yearly_positive['nct_diff']).mean() ) )
print("In positive return years, the difference between CT and non-CT (% mean): {:.2f}".format( (yearly_positive['ct_prcnt'] - yearly_positive['nct_prcnt']).mean() ) )

yearly_negative = yearly_data.loc[ yearly_data['all_diff'] < 0]
print("Number of years housing prices went down: {}".format(yearly_negative['date'].count() ) )
print("In negative return years, the difference between CT and non-CT ($ mean): {:.2f}".format( (yearly_negative['ct_diff'] - yearly_negative['nct_diff']).mean() ) )
print("In negative return years, the difference between CT and non-CT (% mean): {:.2f}".format( (yearly_negative['ct_prcnt'] - yearly_negative['nct_prcnt']).mean() ) )

# 2004 to present yearly data used in statistical significance
post_2004_years = yearly_data.loc[ yearly_data['date'] >= '2003-01-31' ]
yearly_2004_positive = post_2004_years.loc[ (yearly_data['all_diff'] >= 0) ]
yearly_2004_pos_diff_mean = yearly_2004_positive['ct_diff'].mean() - yearly_2004_positive['nct_diff'].mean()
yearly_2004_pos_diff_percent = yearly_2004_positive['ct_prcnt'].mean() - yearly_2004_positive['nct_prcnt'].mean()
print("Since 2004, number of years housing prices went up: {}".format(yearly_2004_positive['date'].count() ) )
print("Since 2004, in positive return years, the difference between CT and non-CT ($ mean): {:.2f}".format(yearly_2004_pos_diff_mean) )
print("Since 2004, in positive return years, the difference between CT and non-CT (% mean): {:.2f}".format(yearly_2004_pos_diff_percent) )

yearly_2004_negative = post_2004_years.loc[ (yearly_data['all_diff'] < 0) ]
yearly_2004_neg_diff_mean = yearly_2004_negative['ct_diff'].mean() - yearly_2004_negative['nct_diff'].mean()
yearly_2004_neg_diff_percent = yearly_2004_negative['ct_prcnt'].mean() - yearly_2004_negative['nct_prcnt'].mean()
print("Since 2004, number of years housing prices went down: {}".format(yearly_2004_negative['date'].count() ) )
print("Since 2004, in negative return years, the difference between CT and non-CT ($ mean): {:.2f}".format(yearly_2004_neg_diff_mean) )
print("Since 2004, in negative return years, the difference between CT and non-CT (% mean): {:.2f}".format(yearly_2004_neg_diff_percent) )

# Display Plot
fig = plt.figure(figsize=(18, 11))
monthly_change_graph = fig.add_subplot(2,2,1)
monthly_diff_plot = fig.add_subplot(2,2,2)
yearly_change_graph = fig.add_subplot(2,2,3)
yearly_diff_plot = fig.add_subplot(2,2,4)

monthly_change_graph.set_title('Fig. 1) Percent change in SFH sale prices from previous month')
monthly_change_graph.set_ylabel('Percent change (%)')
monthly_change_graph.set_xlabel('Date')
monthly_change_graph.plot(monthly_data.date, monthly_data.ct_prcnt, label="College Towns")
monthly_change_graph.plot(monthly_data.date, monthly_data.nct_prcnt, label="Non-College Towns")
monthly_change_graph.axhline(0, color="red", dashes=(1,3))
monthly_change_graph.legend()

monthly_diff_plot.set_title('Fig. 2) Monthly difference in percent change between college and non-college towns\n(positive means collrge towns performed better)')
monthly_diff_plot.set_ylabel('Difference in percent change (%)')
# monthly_diff_plot.set_xlabel('Date')
monthly_diff_plot.axhline(0, color="red", dashes=(1,3))
monthly_diff_plot.scatter(monthly_data.date, monthly_data.ct_prcnt - monthly_data.nct_prcnt)

yearly_change_graph.set_title('Fig. 3) Percent change in SFH sale prices from previous year')
yearly_change_graph.set_ylabel('Percent change (%)')
yearly_change_graph.set_xlabel('Date')
yearly_change_graph.plot(yearly_data.date, yearly_data.ct_prcnt, label="College Towns")
yearly_change_graph.plot(yearly_data.date, yearly_data.nct_prcnt, label="Non-College Towns")
yearly_change_graph.legend()

yearly_diff_plot.set_title('Fig. 4) Yearly difference in percent change between college and non-college towns\n(positive means collrge towns performed better)')
yearly_diff_plot.set_ylabel('Difference in percent change (%)')
yearly_diff_plot.set_xlabel('Date')
yearly_diff_plot.axhline(0, color="red", dashes=(1,3))
yearly_diff_plot.scatter(yearly_data.date, yearly_data.ct_prcnt - yearly_data.nct_prcnt)

plt.show()

difference between CT and non-CT ($ mean): 214.56
difference between CT and non-CT (% mean): 0.08
Standard deviation in monthly return percent: 0.20
Number of months observed: 303
Number of months college towns performed better (higher positive or lower negative returns): 228
Number of months housing prices went up: 233
In positive return months, the difference between CT and non-CT ($ mean): 272.26
In positive return months, the difference between CT and non-CT (% mean): 0.07
Standard deviation in return percent in positive months: 0.12
Number of months housing prices went down: 70
In negative return months, the difference between CT and non-CT ($ mean): 22.50
In negative return months, the difference between CT and non-CT (% mean): 0.10
Standard deviation in return percent in negatie months: 711.33


Number of years observed: 24
Number of years college towns performed better (higher positive or lower negative returns): 18
number of years housing prices went up: 17
In positive return years, the difference between CT and non-CT ($ mean): 2645.43
In positive return years, the difference between CT and non-CT (% mean): 0.82
Number of years housing prices went down: 6
In negative return years, the difference between CT and non-CT ($ mean): 1704.36
In negative return years, the difference between CT and non-CT (% mean): 1.69
Since 2004, number of years housing prices went up: 11
Since 2004, in positive return years, the difference between CT and non-CT ($ mean): 3354.32
Since 2004, in positive return years, the difference between CT and non-CT (% mean): 0.91
Since 2004, number of years housing prices went down: 6
Since 2004, in negative return years, the difference between CT and non-CT ($ mean): 1704.36
Since 2004, in negative return years, the difference between CT and non-CT (% mean): 1.69

Change in home sale price (mean) values. Comparing college and non-college towns

Fig. 1: The difference in home sale prices (mean) from the previous month (i.e. positive values indicate an increase in sale prices whereas negative values indicate a decrease). The college town and the non-college town lines follow each other closely, each overperforming the other at times. It does appear, however, that, overall, the college town returns outperform the non-college town returns. It is worth noting the extreme impact of the Great Recession housing collapse in 2008 that this view illustrates.

Fig. 2: The difference in home sale price changes from the previous month between college towns and non-college towns (college town return minus non-college town return: positive values indicate college towns outperformed non-college towns, and vice versa). We can see that most months, college towns have a slightly higher return (0.1–0.3 percent). College towns especially over-performed their non-college town counterparts during the U.S. housing market correction of 2005.

Fig. 3: The difference in home sale prices (mean) from the previous year. Illustrated the same concept as figure 1, but on a yearly level. This zoomed-out perspective removes some of the noise from the monthly view and shows that college towns do tend to have slightly higher returns than their non-college town counterparts.

Fig. 4: The difference in home sale price changes from the previous year between college towns and non-college towns. The information is the same as in Figure 2, but at a yearly level. Here, we can see that in 19 of the 23 years of data, college towns had better yearly-returns than did non-college towns. If average sale prices went up, college towns went up by more, and, if sale prices went down, college towns went down less in all but four years.

covid_months = data.loc[:,'2020-03-31':'2021-04-30'].columns.tolist()

index = covid_months[1:]
columns = ['nct_mean', 'ct_mean', 'nct_diff', 'ct_diff', 'nct_prcnt', 'ct_prcnt', 'all_mean', 'all_diff']
array = np.zeros( ( len(index), len(columns) ), dtype=float )
covid_monthly_data = pd.DataFrame(array, columns=columns, index=index)

for month, i in zip(covid_months, range(0, len(covid_months)) ):
    # for each month after the first
    if i>0:
        # non-college town
        nct_prev_month = data[prev].loc[ (data[prev] > 0) & (data['colleges_count'] == 0) ].mean()
        nct_this_month = data[month].loc[ (data[month] > 0) & (data['colleges_count'] == 0) ].mean()
        nct_change = nct_this_month - nct_prev_month
        covid_monthly_data.loc[month, 'nct_mean'] = nct_this_month
        covid_monthly_data.loc[month, 'nct_diff'] = nct_change
        covid_monthly_data.loc[month, 'nct_prcnt'] = nct_change / nct_prev_month * 100
        
        # college town
        ct_prev_month = data[prev].loc[ (data[prev] > 0) & (data['colleges_count'] > 0) ].mean()
        ct_this_month = data[month].loc[ (data[month] > 0) & (data['colleges_count'] > 0) ].mean()
        ct_change = ct_this_month - ct_prev_month
        covid_monthly_data.loc[month, 'ct_mean'] = ct_this_month
        covid_monthly_data.loc[month, 'ct_diff'] = ct_change
        covid_monthly_data.loc[month, 'ct_prcnt'] = ct_change / ct_prev_month * 100
        
        # all cities
        all_prev_month = data[prev].loc[ (data[prev] > 0) ].mean()
        all_this_month = data[month].loc[ (data[month] > 0) ].mean()
        all_change = all_this_month - all_prev_month
        covid_monthly_data.loc[month, 'all_mean'] = all_this_month
        covid_monthly_data.loc[month, 'all_diff'] = all_change
    prev = month
    
covid_monthly_data = covid_monthly_data.reset_index()
covid_monthly_data.rename(columns = {'index':'date_str'}, inplace = True) 
covid_monthly_data['date'] = pd.to_datetime(covid_monthly_data['date_str'], format="%Y-%m-%d")
covid_monthly_data.reset_index()

month_pos_diff_percent = (month_negative['ct_prcnt'] - month_negative['nct_prcnt']).mean()
historic_diff_std = (covid_monthly_data.ct_prcnt - covid_monthly_data.nct_prcnt).std()
covid_return_diff = (covid_monthly_data.ct_prcnt - covid_monthly_data.nct_prcnt).mean()
print( "Mean historic difference between college towns and non-college town returns in positve months (%): {:.2f}".format( month_pos_diff_percent ) )
print( "Standard deviation in historic return differences in positve months (%): {:.2f}".format( historic_diff_std ) )
print( "Difference between college towns and non-college towns Since March 2020 (all positive return months) (%): {:.2f}".format( covid_return_diff ) )
print("Number of months in time-period: {} months".format(covid_monthly_data.date.count()))
period_change = (covid_monthly_data['all_mean'][covid_monthly_data.date.count() - 1] - covid_monthly_data['all_mean'][0])
period_start = covid_monthly_data['all_mean'][0]
print("Change over period (% mean): {:.2f}".format( period_change / period_start * 100 ) )

fig = plt.figure(figsize=(18, 5))
covid_change_graph = fig.add_subplot(1,2,1)
covid_diff_plot = fig.add_subplot(1,2,2)

covid_change_graph.set_title('Percent change in SFH sale prices from previous month')
covid_change_graph.set_ylabel('Percent change')
covid_change_graph.set_xlabel('Date')
covid_change_graph.plot(covid_monthly_data['date'], covid_monthly_data.ct_prcnt, label="College Towns")
covid_change_graph.plot(covid_monthly_data['date'], covid_monthly_data.nct_prcnt, label="Non-College Towns")
covid_change_graph.axhline(0, color="red", dashes=(1,3))
covid_change_graph.legend()
locator = mdates.AutoDateLocator(minticks=1, maxticks=12)
formatter = mdates.ConciseDateFormatter(locator)
covid_change_graph.xaxis.set_major_formatter(formatter)

covid_diff_plot.set_title('Differnece in return percentage between college and non-college towns\n(positive means collrge towns performed better)')
covid_diff_plot.set_ylabel('Difference (percents)')
covid_diff_plot.set_xlabel('Date')
covid_diff_plot.axhline( month_pos_diff_percent, color="red", dashes=(1,3), label="Mean historic overperformance of college towns in positve months")
covid_diff_plot.axhline( (covid_monthly_data.ct_prcnt - covid_monthly_data.nct_prcnt).mean(), color="blue", dashes=(1,3), label="Current mean overperformance of college towns")
covid_diff_plot.scatter( covid_monthly_data.date_str, covid_monthly_data.ct_prcnt - covid_monthly_data.nct_prcnt, label="Return difference")
covid_diff_plot.legend()

plt.show()

Mean historic difference between college towns and non-college town returns in positve months (%): 0.10
Standard deviation in historic return differences in positve months (%): 0.04
Difference between college towns and non-college towns Since March 2020 (all positive return months) (%): 0.04
Number of months in time-period: 13 months
Change over period (% mean): 9.83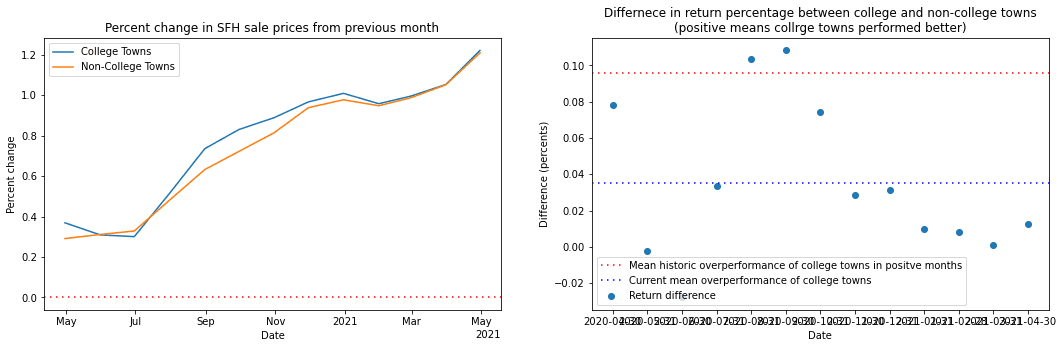

Monthly change in home sale price (mean) during the 2020 COVID-19 pandemic

Over the past thirteen months, home prices have risen by 9.83%, with the average monthly price increase being 0.76%. Historically, homes see an average monthly increase of 0.19% (within the range of this study).

During these thirteen months, college towns have seen a 0.04% higher monthly average than have non-college towns. This is within two standard deviations of the average amount by which college towns overperform non-college towns in the months in which the market as a whole sees positive returns.

Evaluation of significance

college_pop_data_2010 = pd.DataFrame( np.zeros( ( data['pop_2010'].count(), 2 ), dtype=float ), columns=['pop_2010', 'has_college'])
college_pop_data_2010['pop_2010'] = data['pop_2010']
college_pop_data_2010['has_college'] = data['colleges_count'] > 0

college_pop_model_2010 = LinearRegression()
college_pop_model_2010.fit( college_pop_data_2010['has_college'].values.reshape(len(college_pop_data_2010), 1), college_pop_data_2010['pop_2010'].values.reshape(len(college_pop_data_2010), 1))
college_pop_predictions_2010 = college_pop_model_2010.predict( college_pop_data_2010['has_college'].values.reshape(len(college_pop_data_2010), 1) )

print("2010 coef: {:.2f}".format( college_pop_model_2010.coef_[0][0]) )
print("2010 intercept: {:.2f}".format( college_pop_model_2010.intercept_[0]) )
print("2010 r-squared: {:.2f}".format( college_pop_model_2010.score( college_pop_data_2010['has_college'].values.reshape(len(college_pop_data_2010), 1), college_pop_data_2010['pop_2010'].values.reshape(len(college_pop_data_2010), 1))) )

ttest = ttest_ind(college_pop_data_2010.loc[ (college_pop_data_2010['has_college'] == True) ]['pop_2010'], college_pop_data_2010.loc[ (college_pop_data_2010['has_college'] == False) ]['pop_2010'])
ttest_stat = ttest[0]
ttest_pvalue = ttest[1]
print("2010 t-test stat: {:.2f}".format( ttest_stat ) )
print("2010 P-value: {:.10f}".format( ttest_pvalue ) )

college_pop_data_2019 = pd.DataFrame( np.zeros( ( data['pop_2019'].count(), 2 ), dtype=float ), columns=['pop_2019', 'has_college'])
college_pop_data_2019['pop_2019'] = data['pop_2019']
college_pop_data_2019['has_college'] = data['colleges_count'] > 0

college_pop_model_2019 = LinearRegression()
college_pop_model_2019.fit( college_pop_data_2019['has_college'].values.reshape(len(college_pop_data_2019), 1), college_pop_data_2019['pop_2019'].values.reshape(len(college_pop_data_2019), 1))
college_pop_predictions_2019 = college_pop_model_2019.predict( college_pop_data_2019['has_college'].values.reshape(len(college_pop_data_2019), 1) )

print("2019 coef: {:.2f}".format( college_pop_model_2019.coef_[0][0]) )
print("2019 intercept: {:.2f}".format( college_pop_model_2019.intercept_[0]) )
print("2019 r-squared: {:.2f}".format( college_pop_model_2019.score( college_pop_data_2019['has_college'].values.reshape(len(college_pop_data_2019), 1), college_pop_data_2019['pop_2019'].values.reshape(len(college_pop_data_2019), 1))) )

ttest = ttest_ind(college_pop_data_2019.loc[ (college_pop_data_2019['has_college'] == True) ]['pop_2019'], college_pop_data_2019.loc[ (college_pop_data_2019['has_college'] == False) ]['pop_2019'])
ttest_stat = ttest[0]
ttest_pvalue = ttest[1]
print("2019 t-test stat: {:.2f}".format( ttest_stat ) )
print("2019 P-value: {:.10f}".format( ttest_pvalue ) )



fig = plt.figure(figsize=(18, 5))
plt2010 = fig.add_subplot(1,2,1)
plt2019 = fig.add_subplot(1,2,2)

plt2010.scatter( college_pop_data_2010['has_college'], college_pop_data_2010['pop_2010'], alpha=0.3 )
plt2010.plot( college_pop_data_2010['has_college'], college_pop_predictions_2010 )
plt2010.set_xticks( [0, 1])
plt2010.set_title('College town as a predictor of population in 2010')
plt2010.set_ylabel('SFH sale price ($)')
plt2010.set_xlabel('College Town, 0=No, 1=Yes')

plt2019.scatter( college_pop_data_2019['has_college'], college_pop_data_2019['pop_2019'], alpha=0.3 )
plt2019.plot( college_pop_data_2019['has_college'], college_pop_predictions_2019 )
plt2019.set_xticks( [0, 1] )
plt2019.set_title('College town as a predictor of population in  2019')
plt2019.set_ylabel('SFH sale price ($)')
plt2019.set_xlabel('College Town, 0=No, 1=Yes')

plt.show()

2010 coef: 49724.20
2010 intercept: 5936.40
2010 r-squared: 0.21
2010 t-test stat: 67.94
2010 P-value: 0.0000000000
2019 coef: 52882.13
2019 intercept: 6301.94
2019 r-squared: 0.21
2019 t-test stat: 66.70
2019 P-value: 0.0000000000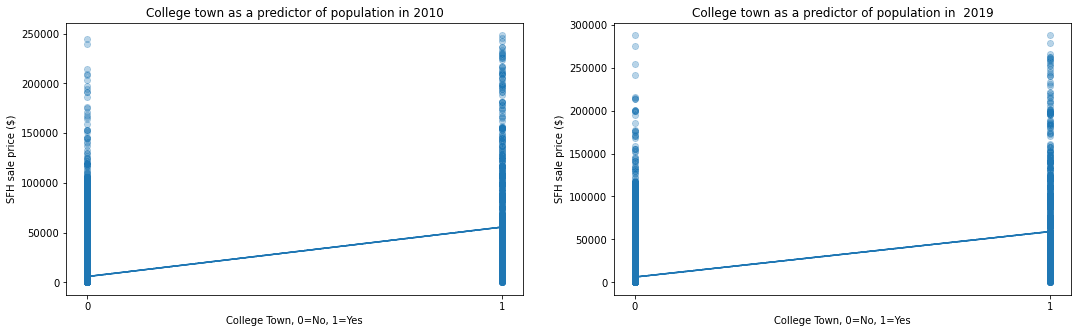

Evaluating the significance of college presence on population size

The presence of a college does turn out to be a strong predictor of a city's population size. In 2010, the presence of a college predicted a city was larger by 6,019 people with an r-squared value of 0.21. Likewise, in 2019, the presence of a college predicted a city was larger by 6,389 people with an r-squared value of 0.21 as well.

For both years, the p-value that the population size difference between the two groups was due to randomness was less than 0.000001, indicating statistical significance for this difference.

Given the difference in population sizes between college towns and non-college towns (all being cities with populations less than 250,000), what role does population size play in home sale values?

years = ['2010', '2019']

for year in years:
    nct_model = LinearRegression()
    nct_x = data.loc[ (data[ year + '-01-31'] > 0) & (data['colleges_count'] == 0) ]['pop_' + year]
    nct_y = data.loc[ (data[ year + '-01-31'] > 0) & (data['colleges_count'] == 0) ][year + '-01-31']
    nct_model.fit( nct_x.values.reshape(len(nct_x), 1), nct_y.values.reshape(len(nct_y), 1) )
    nct_y_predictions = nct_model.predict( nct_x.values.reshape(len(nct_x), 1) )

    ct_model = LinearRegression()
    ct_x = data.loc[ (data[year + '-01-31'] > 0) & (data['colleges_count'] > 0) ]['pop_' + year]
    ct_y = data.loc[ (data[year + '-01-31'] > 0) & (data['colleges_count'] > 0) ][year + '-01-31']
    ct_model.fit( ct_x.values.reshape(len(ct_x), 1), ct_y.values.reshape(len(ct_y), 1) )
    ct_y_predictions = ct_model.predict( ct_x.values.reshape(len(ct_x), 1) )

    all_model = LinearRegression()
    all_x = data.loc[ (data[year + '-01-31'] > 0) ]['pop_' + year]
    all_y = data.loc[ (data[year + '-01-31'] > 0) ][year + '-01-31']
    all_model.fit( all_x.values.reshape(len(all_x), 1), all_y.values.reshape(len(all_y), 1) )
    all_y_predictions = all_model.predict( all_x.values.reshape(len(all_x), 1) )
    
    print(year +" All cities coef: {:.2f}".format( all_model.coef_[0][0] ) )
    print(year +" All cities intercept: {:.2f}".format( all_model.intercept_[0] ) )
    print(year +" Popluation as a predictor of price R-squared value: {:.2f}".format( all_model.score( all_x.values.reshape(len(all_x), 1), all_y.values.reshape(len(all_y), 1) ) ) )

    print(year +" Non-college town coef: {:.2f}".format( nct_model.coef_[0][0] ) )
    print(year +" Non-college town intercept: {:.2f}".format( nct_model.intercept_[0] ) )
    print(year +" Non-college town population R-squared value: {:.2f}".format( nct_model.score( nct_x.values.reshape(len(nct_x), 1), nct_y.values.reshape(len(nct_y), 1) ) ) )
    print(year +" College town coef: {:.2f}".format( ct_model.coef_[0][0] ) )
    print(year +" College town intercept: {:.2f}".format( ct_model.intercept_[0] ) )
    print(year +" College town population R-squared value: {:.2f}".format( ct_model.score( ct_x.values.reshape(len(ct_x), 1), ct_y.values.reshape(len(ct_y), 1) ) ) )

    ttest = ttest_ind(ct_y, nct_y)
    ttest_stat = ttest[0]
    ttest_pvalue = ttest[1]
    print(year +" t-test stat: {:.2f}".format( ttest_stat ) )
    print(year +" P-value: {:.10f}".format( ttest_pvalue ) )
    
    
    fig = plt.figure(figsize=(18, 5))
    plotall = fig.add_subplot(1,2,1)
    plotyear = fig.add_subplot(1,2,2)

    plotall.scatter( data.loc[ (data[year + '-01-31'] > 0) ]['pop_' + year] , data.loc[ (data[year + '-01-31'] > 0)][year + '-01-31'], alpha=0.3, label="all cities <250,000" )
    plotall.plot( data.loc[ (data[year + '-01-31'] > 0) ]['pop_' + year], all_y_predictions )
    plotall.ticklabel_format(style='plain')
    plotall.set_title(year + ' city population size and house sale price')
    plotall.set_ylabel('SFH sale price ($)')
    plotall.set_xlabel('population')
    plotall.legend()

    plotyear.scatter( data.loc[ (data[year + '-01-31'] > 0) & (data['colleges_count'] == 0) ]['pop_' + year] , data.loc[ (data[year + '-01-31'] > 0) & (data['colleges_count'] == 0) ][year + '-01-31'], alpha=0.3, label="non-college town" )
    plotyear.scatter( data.loc[ (data[year + '-01-31'] > 0) & (data['colleges_count'] > 0) ]['pop_' + year] , data.loc[ (data[year + '-01-31'] > 0) & (data['colleges_count'] > 0) ][year + '-01-31'], alpha=0.3, label="college town" )
    plotyear.plot( data.loc[ (data[year + '-01-31'] > 0) & (data['colleges_count'] == 0) ]['pop_' + year], nct_y_predictions )
    plotyear.plot( data.loc[ (data[year + '-01-31'] > 0) & (data['colleges_count'] > 0) ]['pop_' + year], ct_y_predictions )
    plotyear.ticklabel_format(style='plain')
    plotyear.set_title(year + ' city population size and house sale price')
    plotyear.set_ylabel('SFH sale price ($)')
    plotyear.set_xlabel('population')
    plotyear.legend()

    plt.show()

2010 All cities coef: 1.21
2010 All cities intercept: 144805.67
2010 Popluation as a predictor of price R-squared value: 0.02
2010 Non-college town coef: 2.09
2010 Non-college town intercept: 140121.64
2010 Non-college town population R-squared value: 0.02
2010 College town coef: 0.23
2010 College town intercept: 177706.60
2010 College town population R-squared value: 0.01
2010 t-test stat: 4.32
2010 P-value: 0.0000153506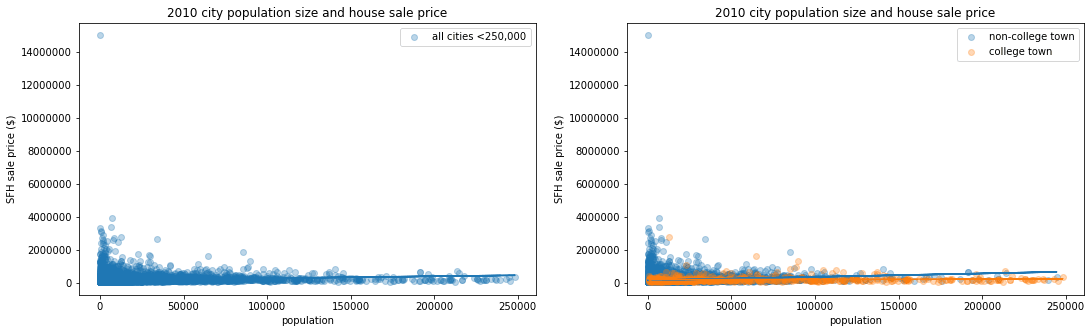

2019 All cities coef: 2.07
2019 All cities intercept: 172861.23
2019 Popluation as a predictor of price R-squared value: 0.02
2019 Non-college town coef: 3.46
2019 Non-college town intercept: 165955.48
2019 Non-college town population R-squared value: 0.03
2019 College town coef: 0.54
2019 College town intercept: 217653.68
2019 College town population R-squared value: 0.02
2019 t-test stat: 5.08
2019 P-value: 0.0000003832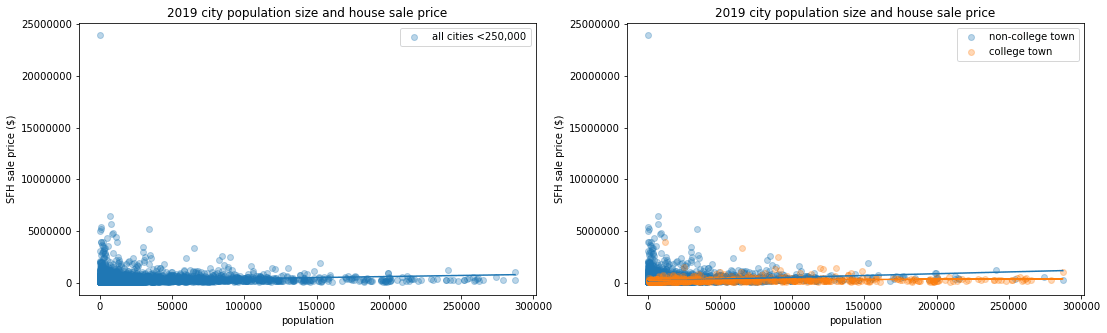

Evaluating the impact of population size on home sale price

Looking at the years 2010 and 2019, we can see that population size is a poor predictor of home sale prices. The above plots show the relationship between population size and home sale prices for both of those years. Despite the existence of numerous small-population-high-value outliers at the low end of the graph, there is a weak positive correlation between the two variables.

In 2010, the coefficient between population and price was 1.21, with an r-squared value of 0.01. In 2019, the population to price coefficient was 2.07 with an r-squared value of 0.02.

Looking at college towns versus non-college towns in the same years, we see similarly low correlations. In 2010, the non-college town coefficient between population and price was 2.09, with an r-squared of 0.02, and for college towns, the coefficient was 0.23, and the r-squared value was 0.01.

In 2019, the non-college town coefficient was 3.46 with an r-squared of 0.03, and for college towns, the coefficient was 0.54, and the r-squared 0.02.

# Negative return years (2008-2013)
neg_all_diff_model = LinearRegression()
neg_all_pop = data.loc[data['2008-01-31'] > 0]['pop_2013']
neg_all_diff = (data.loc[ (data['2008-01-31'] > 0) ]['2013-01-31'] - data.loc[ (data['2008-01-31'] > 0)]['2008-01-31']) / data.loc[ (data['2008-01-31'] > 0)]['2008-01-31'] * 100
neg_all_diff_model.fit( neg_all_pop.values.reshape(len(neg_all_pop), 1), neg_all_diff.values.reshape(len(neg_all_diff), 1) )
neg_all_diff_predictions = neg_all_diff_model.predict( neg_all_pop.values.reshape(len(neg_all_pop), 1) )

neg_ct_diff_model = LinearRegression()
neg_ct_pop = data.loc[ (data['2008-01-31'] > 0) & (data['colleges_count'] > 0) ]['pop_2013']
neg_ct_diff = (data.loc[ (data['2008-01-31'] > 0) & (data['colleges_count'] > 0) ]['2013-01-31'] - data.loc[ (data['2008-01-31'] > 0) & (data['colleges_count'] > 0) ]['2008-01-31']) / data.loc[ (data['2008-01-31'] > 0) & (data['colleges_count'] > 0) ]['2008-01-31'] * 100
neg_ct_diff_model.fit( neg_ct_pop.values.reshape(len(neg_ct_pop), 1), neg_ct_diff.values.reshape(len(neg_ct_diff), 1) )
neg_ct_diff_predictions = neg_ct_diff_model.predict( neg_ct_pop.values.reshape(len(neg_ct_pop), 1) )

neg_nct_diff_model = LinearRegression()
neg_nct_pop = data.loc[ (data['2008-01-31'] > 0) & (data['colleges_count'] == 0) ]['pop_2013']
neg_nct_diff = (data.loc[ (data['2008-01-31'] > 0) & (data['colleges_count'] == 0) ]['2013-01-31'] - data.loc[ (data['2008-01-31'] > 0) & (data['colleges_count'] == 0) ]['2008-01-31']) / data.loc[ (data['2008-01-31'] > 0) & (data['colleges_count'] == 0) ]['2008-01-31'] * 100
neg_nct_diff_model.fit( neg_nct_pop.values.reshape(len(neg_nct_pop), 1), neg_nct_diff.values.reshape(len(neg_nct_diff), 1) )
neg_nct_diff_predictions = neg_nct_diff_model.predict( neg_nct_pop.values.reshape(len(neg_nct_pop), 1) )

# Positive return years (2013-2018)
pos_all_diff_model = LinearRegression()
pos_all_pop = data.loc[ (data['2013-01-31'] > 0)]['pop_2018']
pos_all_diff = (data.loc[ (data['2013-01-31'] > 0)]['2018-01-31'] - data.loc[ (data['2013-01-31'] > 0)]['2013-01-31']) / data.loc[ (data['2013-01-31'] > 0)]['2013-01-31'] * 100
pos_all_diff_model.fit( pos_all_pop.values.reshape(len(pos_all_pop), 1), pos_all_diff.values.reshape(len(pos_all_diff), 1) )
pos_all_diff_predictions = pos_all_diff_model.predict( pos_all_pop.values.reshape(len(pos_all_pop), 1) )

pos_ct_diff_model = LinearRegression()
pos_ct_pop = data.loc[ (data['2013-01-31'] > 0) & (data['colleges_count'] > 0) ]['pop_2018']
pos_ct_diff = (data.loc[ (data['2013-01-31'] > 0) & (data['colleges_count'] > 0) ]['2018-01-31'] - data.loc[ (data['2013-01-31'] > 0) & (data['colleges_count'] > 0) ]['2013-01-31']) / data.loc[ (data['2013-01-31'] > 0) & (data['colleges_count'] > 0) ]['2013-01-31'] * 100
pos_ct_diff_model.fit( pos_ct_pop.values.reshape(len(pos_ct_pop), 1), pos_ct_diff.values.reshape(len(pos_ct_diff), 1) )
pos_ct_diff_predictions = pos_ct_diff_model.predict( pos_ct_pop.values.reshape(len(pos_ct_pop), 1) )

pos_nct_diff_model = LinearRegression()
pos_nct_pop = data.loc[ (data['2013-01-31'] > 0) & (data['colleges_count'] == 0) ]['pop_2018']
pos_nct_diff = (data.loc[ (data['2013-01-31'] > 0) & (data['colleges_count'] == 0) ]['2018-01-31'] - data.loc[ (data['2013-01-31'] > 0) & (data['colleges_count'] == 0) ]['2013-01-31']) / data.loc[ (data['2013-01-31'] > 0) & (data['colleges_count'] == 0) ]['2013-01-31'] * 100
pos_nct_diff_model.fit( pos_nct_pop.values.reshape(len(pos_nct_pop), 1), pos_nct_diff.values.reshape(len(pos_nct_diff), 1) )
pos_nct_diff_predictions = pos_nct_diff_model.predict( pos_nct_pop.values.reshape(len(pos_nct_pop), 1) )

print("Negative years (2008-2013) CT mean % price change: {:.8f}".format( neg_ct_diff.mean() ) )
print("Negative years (2008-2013) NCT mean % price change: {:.8f}".format( neg_nct_diff.mean() ) )
print("Negative years (2008-2013) CT population price coef: {:.8f}".format( neg_ct_diff_model.coef_[0][0] ) )
print("Negative years (2008-2013) NCT coef: {:.8f}".format( neg_nct_diff_model.coef_[0][0] ) )
print("Negative years (2008-2013) CT y intercept: {:.4f}".format( neg_ct_diff_model.intercept_[0] ) )
print("Negative years (2008-2013) NCT intercept: {:.4f}".format( neg_nct_diff_model.intercept_[0] ) )
print("Negative years (2008-2013) All population R-squared value: {:.4f}".format( neg_all_diff_model.score( neg_all_pop.values.reshape(len(neg_all_pop), 1), neg_all_diff.values.reshape(len(neg_all_diff), 1) ) ) )
print("Negative years (2008-2013) CT population R-squared value: {:.4f}".format( neg_ct_diff_model.score( neg_ct_pop.values.reshape(len(neg_ct_pop), 1), neg_ct_diff.values.reshape(len(neg_ct_diff), 1) ) ) )
print("Negative years (2008-2013) NCT population R-squared value: {:.4f}".format( neg_nct_diff_model.score( neg_nct_pop.values.reshape(len(neg_nct_pop), 1), neg_nct_diff.values.reshape(len(neg_nct_diff), 1) ) ) )
neg_ttest = ttest_ind(neg_nct_diff, neg_ct_diff)
neg_ttest_stat = neg_ttest[0]
neg_ttest_pvalue = neg_ttest[1]
print("Negative years (2008-2013) t-test stat: {:.8f}".format( neg_ttest_stat ) )
print("Negative years (2008-2013) P-value: {:.18f}".format( neg_ttest_pvalue ) )
print("\n")

print("Positive years (2013-2018) CT mean % price change: {:.8f}".format( pos_ct_diff.mean() ) )
print("Positive years (2013-2018) NCT mean % price change: {:.8f}".format( pos_nct_diff.mean() ) )
print("Positive years (2013-2018) CT population price coef: {:.8f}".format( pos_ct_diff_model.coef_[0][0] ) )
print("Positive years (2013-2018) NCT coef: {:.8f}".format( pos_nct_diff_model.coef_[0][0] ) )
print("Positive years (2013-2018) CT y intercept: {:.4f}".format( pos_ct_diff_model.intercept_[0] ) )
print("Positive years (2013-2018) NCT intercept: {:.4f}".format( pos_nct_diff_model.intercept_[0] ) )
print("Positive years (2013-2018) All population R-squared value: {:.4f}".format( pos_all_diff_model.score( pos_all_pop.values.reshape(len(pos_all_pop), 1), pos_all_diff.values.reshape(len(pos_all_diff), 1) ) ) )
print("Positive years (2013-2018) CT population R-squared value: {:.4f}".format( pos_ct_diff_model.score( pos_ct_pop.values.reshape(len(pos_ct_pop), 1), pos_ct_diff.values.reshape(len(pos_ct_diff), 1) ) ) )
print("Positive years (2013-2018) NCT population R-squared value: {:.4f}".format( pos_nct_diff_model.score( pos_nct_pop.values.reshape(len(pos_nct_pop), 1), pos_nct_diff.values.reshape(len(pos_nct_diff), 1) ) ) )
pos_ttest = ttest_ind(pos_nct_diff, pos_ct_diff)
pos_ttest_stat = pos_ttest[0]
pos_ttest_pvalue = pos_ttest[1]
print("Positive years (2013-2018) t-test stat: {:.8f}".format( pos_ttest_stat ) )
print("Positive years (2013-2018) P-value: {:.18f}".format( pos_ttest_pvalue ) )
print("\n")

fig = plt.figure(figsize=(18, 5))
plotneg = fig.add_subplot(1,2,1)
plotpos = fig.add_subplot(1,2,2)

plotneg.scatter( neg_nct_pop , neg_nct_diff , alpha=0.3, label="Non-college towns" )
plotneg.plot( neg_nct_pop, neg_nct_diff_predictions )
plotneg.scatter( neg_ct_pop , neg_ct_diff , alpha=0.3, label="College towns" )
plotneg.plot( neg_ct_pop, neg_ct_diff_predictions )
plotneg.axhline(0, color="black", dashes=(1,3))
plotneg.ticklabel_format(style='plain')
plotneg.set_title('Return on SFH price between 2008 and 2013')
plotneg.set_ylabel('change in SFH sale price (%)')
plotneg.set_xlabel('population (2013)')
plotneg.legend()

plotpos.scatter( pos_nct_pop , pos_nct_diff , alpha=0.3, label="Non-college towns" )
plotpos.plot( pos_nct_pop, pos_nct_diff_predictions )
plotpos.scatter( pos_ct_pop , pos_ct_diff , alpha=0.3, label="College towns" )
plotpos.plot( pos_ct_pop, pos_ct_diff_predictions )
plotpos.axhline(0, color="black", dashes=(1,3))
plotpos.ticklabel_format(style='plain')
plotpos.set_title('Return on SFH price between 2013 and 2018')
plotpos.set_ylabel('change in SFH sale price (%)')
plotpos.set_xlabel('population (2018)')
plotpos.legend()

plt.show()

Negative years (2008-2013) CT mean % price change: -13.53420315
Negative years (2008-2013) NCT mean % price change: -12.06645430
Negative years (2008-2013) CT population price coef: -0.00005838
Negative years (2008-2013) NCT coef: -0.00019421
Negative years (2008-2013) CT y intercept: -10.0945
Negative years (2008-2013) NCT intercept: -10.7485
Negative years (2008-2013) All population R-squared value: 0.0340
Negative years (2008-2013) CT population R-squared value: 0.0633
Negative years (2008-2013) NCT population R-squared value: 0.0471
Negative years (2008-2013) t-test stat: 2.53458054
Negative years (2008-2013) P-value: 0.011268381056116019


Positive years (2013-2018) CT mean % price change: 26.95518640
Positive years (2013-2018) NCT mean % price change: 25.72446551
Positive years (2013-2018) CT population price coef: 0.00008078
Positive years (2013-2018) NCT coef: 0.00028841
Positive years (2013-2018) CT y intercept: 22.1387
Positive years (2013-2018) NCT intercept: 23.8066
Positive years (2013-2018) All population R-squared value: 0.0431
Positive years (2013-2018) CT population R-squared value: 0.0704
Positive years (2013-2018) NCT population R-squared value: 0.0636
Positive years (2013-2018) t-test stat: -1.65642201
Positive years (2013-2018) P-value: 0.097656101348085764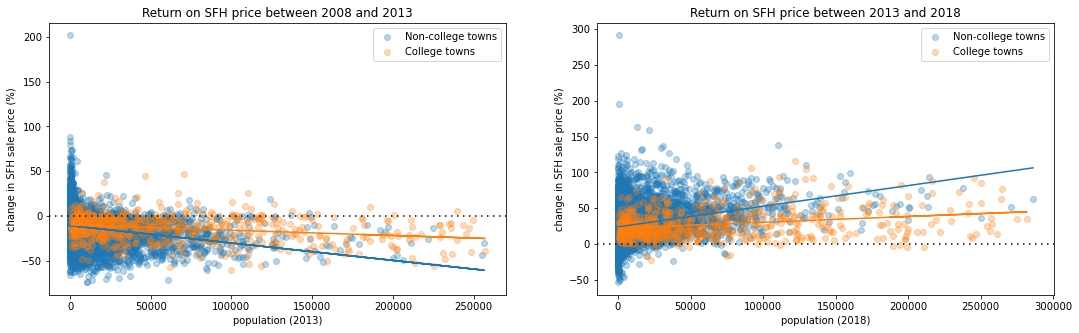

Evaluating the impact of population size on change in home sale prices

Just as in the case of absolute home sale prices, population size has a negligible correlation with percent change in home prices. This is true for non-college towns and college towns in both periods of valuation growth and decline.

Examining two distinct five-year periods, namely, 2008-2013, which saw an overall decline in home prices in each of these five years, and 2013-2018, which saw positive returns each year, we see a similar pattern. During both periods, population size is an equally poor predictor of home prices for both college and non-college towns, but for both periods, its effect is larger for the non-college town group.

During the negative years, population size accounted for 6.33% of the change in home prices for college towns and 4.71% for non-college towns. During the positive years, population size accounted for 6.36% of the change in home prices for college towns and 7.04% for college towns.

During both periods, however, the effect of population size was larger (steeper slope) in the non-college towns than in the college towns. During the negative years (2008-2013) the coefficient of price change to population size was 3.32 times higher for the non-college towns. Likewise, in the positive growth years (2013-2018) it was 3.57 times larger for the non-college towns.

Positive years have significantly more noise in the data. The likelihood that the difference between the college town and non-college town groups was the result of chance compared to being distinctly different groups during negative years had a p-value of 0.011, compared to positive years with a p-value of 0.97.

college_price_data_2010 = pd.DataFrame( np.zeros( ( data['2010-01-31'].count(), 2 ), dtype=float ), columns=['price', 'has_college'])
college_price_data_2010['price'] = data['2010-01-31']
college_price_data_2010['has_college'] = data['colleges_count'] > 0

college_price_model_2010 = LinearRegression()
college_price_model_2010.fit( college_price_data_2010['has_college'].values.reshape(len(college_price_data_2010), 1), college_price_data_2010['price'].values.reshape(len(college_price_data_2010), 1))
college_price_predictions_2010 = college_price_model_2010.predict( college_price_data_2010['has_college'].values.reshape(len(college_price_data_2010), 1) )

print("2010 coef: {:.2f}".format( college_price_model_2010.coef_[0][0]) )
print("2010 intercept: {:.2f}".format( college_price_model_2010.intercept_[0]) )
print("2010 r-squared: {:.4f}".format( college_price_model_2010.score( college_price_data_2010['has_college'].values.reshape(len(college_price_data_2010), 1), college_price_data_2010['price'].values.reshape(len(college_price_data_2010), 1))) )

ttest = ttest_ind(college_price_data_2010.loc[ (college_price_data_2010['has_college'] == False) ]['price'], college_price_data_2010.loc[ (college_price_data_2010['has_college'] == True) ]['price'])
ttest_stat = ttest[0]
ttest_pvalue = ttest[1]
print("2010 t-test stat: {:.2f}".format( ttest_stat ) )
print("2010 P-value: {:.10f}".format( ttest_pvalue ) )

college_price_data_2019 = pd.DataFrame( np.zeros( ( data['2019-01-31'].count(), 2 ), dtype=float ), columns=['price', 'has_college'])
college_price_data_2019['price'] = data['2019-01-31']
college_price_data_2019['has_college'] = data['colleges_count'] > 0

college_price_model_2019 = LinearRegression()
college_price_model_2019.fit( college_price_data_2019['has_college'].values.reshape(len(college_price_data_2019), 1), college_price_data_2019['price'].values.reshape(len(college_price_data_2019), 1))
college_price_predictions_2019 = college_price_model_2019.predict( college_price_data_2019['has_college'].values.reshape(len(college_price_data_2019), 1) )

print("2019 coef: {:.2f}".format( college_price_model_2019.coef_[0][0]) )
print("2019 intercept: {:.2f}".format( college_price_model_2019.intercept_[0]) )
print("2019 r-squared: {:.4f}".format( college_price_model_2019.score( college_price_data_2019['has_college'].values.reshape(len(college_price_data_2019), 1), college_price_data_2019['price'].values.reshape(len(college_price_data_2019), 1))) )

ttest = ttest_ind(college_price_data_2019.loc[ (college_price_data_2019['has_college'] == False) ]['price'], college_price_data_2019.loc[ (college_price_data_2019['has_college'] == True) ]['price'])
ttest_stat = ttest[0]
ttest_pvalue = ttest[1]
print("2019 t-test stat: {:.2f}".format( ttest_stat ) )
print("2019 P-value: {:.10f}".format( ttest_pvalue ) )



fig = plt.figure(figsize=(18, 5))
plt2010 = fig.add_subplot(1,2,1)
plt2019 = fig.add_subplot(1,2,2)

plt2010.scatter( college_price_data_2010['has_college'], college_price_data_2010['price'], alpha=0.3 )
plt2010.plot( college_price_data_2010['has_college'], college_price_predictions_2010 )
plt2010.set_xticks( [0, 1])
plt2010.ticklabel_format(style='plain')
plt2010.set_title('College town as a predictor of Home Sale Price in 2010')
plt2010.set_ylabel('SFH sale price ($)')
plt2010.set_xlabel('College Town, 0=No, 1=Yes')

plt2019.scatter( college_price_data_2019['has_college'], college_price_data_2019['price'], alpha=0.3 )
plt2019.plot( college_price_data_2019['has_college'], college_price_predictions_2019 )
plt2019.set_xticks( [0, 1] )
plt2019.ticklabel_format(style='plain')
plt2019.set_title('College town as a predictor of Home Sale Price in 2019')
plt2019.set_ylabel('SFH sale price ($)')
plt2019.set_xlabel('College Town, 0=No, 1=Yes')

plt.show()

2010 coef: 47598.69
2010 intercept: 137305.47
2010 r-squared: 0.0020
2010 t-test stat: -5.84
2010 P-value: 0.0000000052
2019 coef: 61749.19
2019 intercept: 187577.98
2019 r-squared: 0.0015
2019 t-test stat: -5.10
2019 P-value: 0.0000003490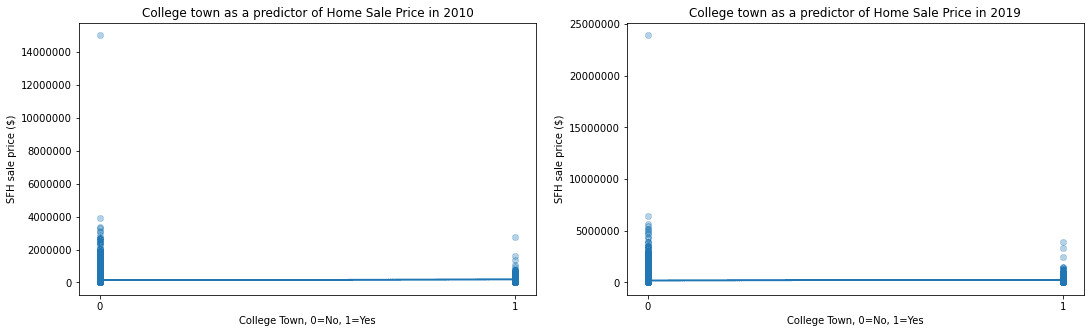

Evaluating the significance of the presence of a college in a city for its home sale prices

The existence of a college in a city does not in itself have a strong correlation with raw home sale prices.

In 2010, the presence of a college predicted the mean home sale price as $47,598.69 higher, but with an r-squared value of close to zero (0.002). In 2019, the presence of a college predicted a higher mean home sale price of $61,749.19, but again, with an r-squared value of close to zero (0.0015).

For both years, the p-value between the two sets was well below 0.0001, indicating the statistical validity of the result.

negative_change = (data[(data['2004-01-31'] > 0)]['2013-01-31'] - data[(data['2004-01-31'] > 0)]['2008-01-31']) / data[(data['2004-01-31'] > 0)]['2008-01-31'] * 100
positive_change = (data[(data['2004-01-31'] > 0)]['2018-01-31'] - data[(data['2004-01-31'] > 0)]['2013-01-31']) / data[(data['2004-01-31'] > 0)]['2013-01-31'] * 100
all_change = (data[(data['2004-01-31'] > 0)]['2021-01-31'] - data[(data['2004-01-31'] > 0)]['2004-01-31']) / data[(data['2004-01-31'] > 0)]['2004-01-31'] * 100
has_college = data[(data['2004-01-31'] > 0)]['colleges_count'] > 0

negative_change = negative_change.reset_index().rename(columns = {0:'neg_change'})
positive_change = positive_change.reset_index().rename(columns = {0:'pos_change'})
all_change = all_change.reset_index().rename(columns = {0:'all_change'})

has_college = has_college.reset_index().rename(columns = {'colleges_count':'has_college'})

diff_table = pd.merge( all_change, negative_change, how='left', on='index')
diff_table = pd.merge( diff_table, positive_change, how='left', on='index')
diff_table = pd.merge( diff_table, has_college, how='left', on='index').drop(columns=['index'])

diff_table['has_college'].fillna(False, inplace=True)

negative_diff_model = LinearRegression()
negative_diff_model.fit( diff_table['has_college'].values.reshape(len(diff_table), 1), diff_table['neg_change'].values.reshape(len(diff_table), 1))
negative_diff_predictions = negative_diff_model.predict( diff_table['has_college'].values.reshape(len(diff_table), 1) )
neg_ttest = ttest_ind( diff_table[(diff_table['has_college'] == False)]['neg_change'], diff_table[(diff_table['has_college'] == True)]['neg_change'])
neg_ttest_stat = neg_ttest[0]
neg_ttest_pvalue = neg_ttest[1]
print("negative years (2008-2013) coef: {:.2f}".format( negative_diff_model.coef_[0][0]) )
print("negative years (2008-2013) intercept: {:.2f}".format( negative_diff_model.intercept_[0]) )
print("negative years (2008-2013) r-squared: {:.4f}".format( negative_diff_model.score( diff_table['has_college'].values.reshape(len(diff_table), 1), diff_table['neg_change'].values.reshape(len(diff_table), 1))) )
print("negative years (2008-2013) t-test stat: {:.2f}".format( neg_ttest_stat ) )
print("negative years (2008-2013) P-value: {:.4f}".format( neg_ttest_pvalue ) )

positive_diff_model = LinearRegression()
positive_diff_model.fit( diff_table['has_college'].values.reshape(len(diff_table), 1), diff_table['pos_change'].values.reshape(len(diff_table), 1))
positive_diff_predictions = positive_diff_model.predict( diff_table['has_college'].values.reshape(len(diff_table), 1) )
pos_ttest = ttest_ind( diff_table[(diff_table['has_college'] == False)]['pos_change'], diff_table[(diff_table['has_college'] == True)]['pos_change'])
pos_ttest_stat = pos_ttest[0]
pos_ttest_pvalue = pos_ttest[1]
print("positive years (2013-2018) coef: {:.2f}".format( positive_diff_model.coef_[0][0]) )
print("positive years (2013-2018) intercept: {:.2f}".format( positive_diff_model.intercept_[0]) )
print("positive years (2013-2018) r-squared: {:.4f}".format( positive_diff_model.score( diff_table['has_college'].values.reshape(len(diff_table), 1), diff_table['pos_change'].values.reshape(len(diff_table), 1))) )
print("positive years (2013-2018) t-test stat: {:.2f}".format( pos_ttest_stat ) )
print("positive years (2013-2018) P-value: {:.4f}".format( pos_ttest_pvalue ) )

all_diff_model = LinearRegression()
all_diff_model.fit( diff_table['has_college'].values.reshape(len(diff_table), 1), diff_table['pos_change'].values.reshape(len(diff_table), 1))
all_diff_predictions = all_diff_model.predict( diff_table['has_college'].values.reshape(len(diff_table), 1) )
all_ttest = ttest_ind( diff_table[(diff_table['has_college'] == False)]['pos_change'], diff_table[(diff_table['has_college'] == True)]['pos_change'])
all_ttest_stat = all_ttest[0]
all_ttest_pvalue = all_ttest[1]
print("all years (2004-2021) coef: {:.2f}".format( all_diff_model.coef_[0][0]) )
print("all years (2004-2021) intercept: {:.2f}".format( all_diff_model.intercept_[0]) )
print("all years (2004-2021) r-squared: {:.4f}".format( all_diff_model.score( diff_table['has_college'].values.reshape(len(diff_table), 1), diff_table['all_change'].values.reshape(len(diff_table), 1))) )
print("all years (2004-2021) t-test stat: {:.2f}".format( all_ttest_stat ) )
print("all years (2004-2021) P-value: {:.4f}".format( all_ttest_pvalue ) )

fig = plt.figure(figsize=(18, 10))
pltneg = fig.add_subplot(2,2,1)
pltpos = fig.add_subplot(2,2,2)
pltall = fig.add_subplot(2,2,3)

pltneg.scatter( diff_table['has_college'], diff_table['neg_change'], alpha=0.3 )
pltneg.plot( diff_table['has_college'], negative_diff_predictions )
pltneg.set_xticks( [0, 1] )
pltneg.ticklabel_format(style='plain')
pltneg.set_title('College town as a predictor of Home Sale change change from 2008-2013')
pltneg.set_ylabel('SFH sale change (%)')
pltneg.set_xlabel('College Town, 0=No, 1=Yes')

pltpos.scatter( diff_table['has_college'], diff_table['pos_change'], alpha=0.3 )
pltpos.plot( diff_table['has_college'], positive_diff_predictions )
pltpos.set_xticks( [0, 1])
pltpos.ticklabel_format(style='plain')
pltpos.set_title('College town as a predictor of Home Sale Price change from 2013-2018')
pltpos.set_ylabel('SFH sale change (%)')
pltpos.set_xlabel('College Town, 0=No, 1=Yes')

pltall.scatter( diff_table['has_college'], diff_table['all_change'], alpha=0.3 )
pltall.plot( diff_table['has_college'], all_diff_predictions )
pltall.set_xticks( [0, 1])
pltall.ticklabel_format(style='plain')
pltall.set_title('College town as a predictor of Home Sale Price change from 2004-2021')
pltall.set_ylabel('SFH sale change (%)')
pltall.set_xlabel('College Town, 0=No, 1=Yes')

plt.show()

negative years (2008-2013) coef: -1.03
negative years (2008-2013) intercept: -14.52
negative years (2008-2013) r-squared: 0.0003
negative years (2008-2013) t-test stat: 1.59
negative years (2008-2013) P-value: 0.1110
positive years (2013-2018) coef: 1.01
positive years (2013-2018) intercept: 27.09
positive years (2013-2018) r-squared: 0.0001
positive years (2013-2018) t-test stat: -1.14
positive years (2013-2018) P-value: 0.2543
all years (2004-2021) coef: 1.01
all years (2004-2021) intercept: 27.09
all years (2004-2021) r-squared: -0.5014
all years (2004-2021) t-test stat: -1.14
all years (2004-2021) P-value: 0.2543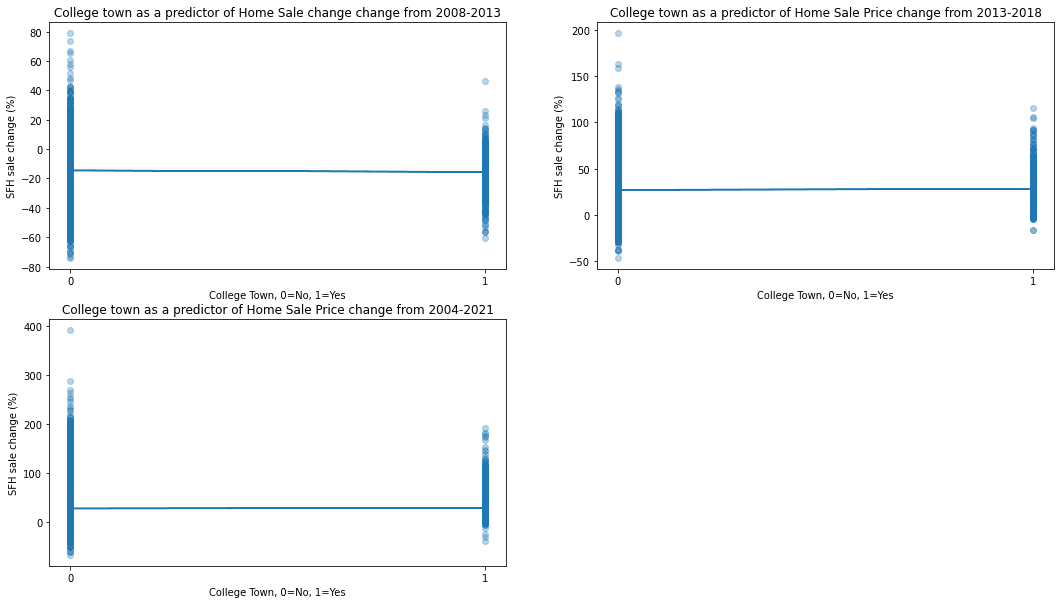

Evaluating the significance of the presence of a college in a city for changes in home sale prices

Here we examine the same distinct five-year periods as before—2008-2013, which saw an overall decline in home prices in each of these five years, and 2013-2018, which saw positive overall returns—this time, evaluating the significance for a city of its status as a college town in terms of predicting change in home prices between the beginning and end of each of the above periods.

During the period of negative housing price changes, the presence of a college in a city predicts a 1.03% worse return over this period, whereas, during the period of positive price change, the presence of a college in a city predicts a 1.01% higher return. Over both periods, the r-squared values were less than 0.01, indicating that the effect of a city being a college town was weak. During the period of negative growth, the probability that the difference between the two groups was not arbitrary was significant, with a p-value of less than 0.01. In terms of the positive-return period, however, we cannot confidently rule out the possibility that the results were arbitrary due to the p-value being 0.25. Examining changes in sale prices over an even longer date range, from 2004-2020, we find that college towns as a predictor of price are even worse than in the smaller samples, with negative r-squared values.

data_zillow = data.loc[:, '1996-01-31':'2021-04-30']
columns = ['date', 'city_count', 'price_mean', 'price_std', 'nct_return', 'ct_return', 'returns_prcnt', 'returns_prcnt_std', 'return_tstat', 'return_pvalue']
index = list(data_zillow.columns)
array = np.zeros( ( len(index), len(columns) ) )
monthly_summary_data = pd.DataFrame(array, columns=columns, index=index)

for i in range( 0, len(months) ):
    monthly_summary_data['city_count'][months[i]] = data_zillow.loc[ data_zillow[months[i]] > 0].shape[0]
    monthly_summary_data['price_mean'] = data_zillow.loc[ data_zillow[months[i]] > 0].mean()
    monthly_summary_data['price_std'] = data_zillow.loc[ data_zillow[months[i]] > 0].std()
    if i > 0:
        nct_last_month = data.loc[ (data['colleges_count'] == 0) & (data[months[i-1]] > 0) ][months[i-1]]
        nct_this_month = data.loc[ (data['colleges_count'] == 0) & (data[months[i-1]] > 0) ][months[i]]
        ct_last_month = data.loc[ (data['colleges_count'] > 0) & (data[months[i-1]] > 0) ][months[i-1]]
        ct_this_month = data.loc[ (data['colleges_count'] > 0) & (data[months[i-1]] > 0) ][months[i]]
        nct_returns = (nct_this_month - nct_last_month) / nct_last_month * 100
        ct_returns = (ct_this_month - ct_last_month) / ct_last_month * 100
        last_month = data.loc[(data[months[i-1]] > 0)][months[i-1]]
        this_month = data.loc[(data[months[i-1]] > 0)][months[i]]
        returns = this_month - last_month
        returns_prcnt = returns / last_month * 100
        ttest = ttest_ind(nct_last_month, ct_last_month)
        ttest_stat = ttest[0]
        ttest_pvalue = ttest[1]
        monthly_summary_data['nct_return'][months[i]] = nct_returns.mean()
        monthly_summary_data['ct_return'][months[i]] = ct_returns.mean()
        monthly_summary_data['returns_prcnt'][months[i]] = returns_prcnt.mean()
        monthly_summary_data['returns_prcnt_std'][months[i]] = returns_prcnt.std()
        monthly_summary_data['return_tstat'][months[i]] = ttest_stat
        monthly_summary_data['return_pvalue'][months[i]] = ttest_pvalue

monthly_summary_data['date'] = pd.to_datetime(monthly_summary_data.index, format="%Y-%m-%d")


print( "1997 number of cities with data: {:.0f}".format(monthly_summary_data['city_count']['1996-02-29'] ) )
print( "1997 p-value of price difference between NCT and CT: {:.8f}".format(monthly_summary_data['return_pvalue']['1996-02-29'] ) )
print( "1999 number of cities with data: {:.0f}".format(monthly_summary_data['city_count']['1999-02-28'] ) )
print( "1999 p-value of price difference between NCT and CT: {:.8f}".format(monthly_summary_data['return_pvalue']['1999-02-28'] ) )
print( "2004 number of cities with data: {:.0f}".format(monthly_summary_data['city_count']['2004-02-29'] ) )
print( "2004 p-value of price difference between NCT and CT: {:.8f}".format(monthly_summary_data['return_pvalue']['2004-02-29'] ) )
print( "2009 number of cities with data: {:.0f}".format(monthly_summary_data['city_count']['2009-02-28'] ) )
print( "2009 p-value of price difference between NCT and CT: {:.8f}".format(monthly_summary_data['return_pvalue']['2009-02-28'] ) )
print( "2014 number of cities with data: {:.0f}".format(monthly_summary_data['city_count']['2014-02-28'] ) )
print( "2014 p-value of price difference between NCT and CT: {:.8f}".format(monthly_summary_data['return_pvalue']['2014-02-28'] ) )
print( "2019 number of cities with data: {:.0f}".format(monthly_summary_data['city_count']['2019-02-28'] ) )
print( "2019 p-value of price difference between NCT and CT: {:.8f}".format(monthly_summary_data['return_pvalue']['2019-02-28'] ) )

fig = plt.figure(figsize=(18, 6))
p_plot = fig.add_subplot(1,1,1)
p_plot.plot(monthly_summary_data['date'][1:], monthly_summary_data['city_count'][1:] / monthly_summary_data['city_count'][1:].max(), label="number of cities included in p-value calculation (proportion of full set / 100)")
p_plot.plot(monthly_summary_data['date'][1:], monthly_summary_data['return_pvalue'][1:], label="p-value of return percent difference")
p_plot.plot(monthly_summary_data['date'][1:], ( (monthly_summary_data['ct_return'][1:] - monthly_summary_data['nct_return'][1:]) ), label="difference between CT and NCT percent returns (postitive means CT performed better)" )
p_plot.axhline(0.05, color="orange", dashes=(1,3), label="p-value of 0.05 threshold")
p_plot.axhline(0, color="gray", dashes=(1,3), label="zero")
p_plot.set_ylabel('Percent')
p_plot.set_xlabel('Date')
p_plot.legend()
plt.show()

ct_wins = monthly_summary_data.loc[ (monthly_summary_data['date'] > '2004-01-31') & (monthly_summary_data['ct_return'] > monthly_summary_data['nct_return'])]
nct_wins = monthly_summary_data.loc[ (monthly_summary_data['date'] > '2004-01-31') & (monthly_summary_data['ct_return'] < monthly_summary_data['nct_return'])]
ct_returns = monthly_summary_data.loc[monthly_summary_data['date'] > '2004-01-31']['ct_return']
nct_returns = monthly_summary_data.loc[monthly_summary_data['date'] > '2004-01-31']['nct_return']

print("Since 2004, months college towns return higher: ", ct_wins.shape[0] )
print("Since 2004, months non-college towns return higher: ", nct_wins.shape[0] )
print("Since 2004, mean college town monthly return: {:.2f}%".format(ct_returns.mean() ) )
print("Since 2004, mean non-college town monthly return: {:.2f}%".format(nct_returns.mean() ) )
print("Since 2004, college town monthly return standard deviation: {:.2f}%".format(ct_returns.std() ) )
print("Since 2004, non-college town monthly return standard deviation: {:.2f}%".format(nct_returns.std() ) )
ttest = ttest_ind(ct_returns, nct_returns)
ttest_stat = ttest[0]
ttest_pvalue = ttest[1]
print("T-test score of monthly returns for college towns compared to non-college towns: {:.2f}".format(ttest_stat ) )
print("P-value monthly returns for college towns are distinct from non-college towns: {:.2f}".format(ttest_pvalue ) )

1997 number of cities with data: 7310
1997 p-value of price difference between NCT and CT: 0.41897583
1999 number of cities with data: 8276
1999 p-value of price difference between NCT and CT: 0.28346877
2004 number of cities with data: 9867
2004 p-value of price difference between NCT and CT: 0.08164846
2009 number of cities with data: 15081
2009 p-value of price difference between NCT and CT: 0.00003891
2014 number of cities with data: 16187
2014 p-value of price difference between NCT and CT: 0.00004670
2019 number of cities with data: 17073
2019 p-value of price difference between NCT and CT: 0.00000038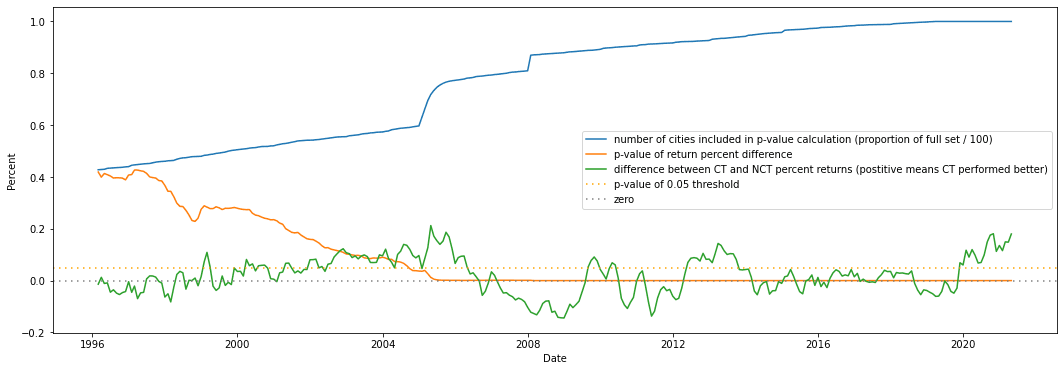

Since 2004, months college towns return higher:  116
Since 2004, months non-college towns return higher:  91
Since 2004, mean college town monthly return: 0.23%
Since 2004, mean non-college town monthly return: 0.21%
Since 2004, college town monthly return standard deviation: 0.41%
Since 2004, non-college town monthly return standard deviation: 0.35%
T-test score of monthly returns for college towns compared to non-college towns: 0.46
P-value monthly returns for college towns are distinct from non-college towns: 0.65

Evaluating the significance of the difference between college towns and non-college towns

The above plot illustrates three values:

The p-value for the difference in home sale price change from the previous month between college and non-college towns.
The difference in college town returns (%) from the previous month compared to the monthly return of non-college towns—the difference expressed as a non-negative, absolute value.
The relative number of cities with sale price data used to calculate the difference in the returns between college towns and non-college towns. In the earliest dates considered in this study, the included sample size comprised only about 40% of the eventual total sample size. This value is expressed as a percentage of the final count divided by 100 to fit on the same axis scale.

As can be seen, the difference between CT and NCT home sale values do not meet the criteria for statistical significance (p-value < 0.05) until February 2004, when enough observations are added to the sample size that the p-value crosses the 0.05 statistical threshold.

In terms of the 207 months since February 2004, home values in college towns have performed better than in non-college towns within 116 of these months, non-college towns seeing higher returns within the remaining 91 months. On a monthly level, the difference between college and non-college towns is statistically significant.

The percentage of months that college towns performed better (27.4%) does not, however, turn out to be statistically significant, with the probability that this could be a random result of 0.65.

Interpretation and conclusions

Evaluating the difference between college and non-college town changes in home sale prices

Historic data shows that purchasing a home in a college town has been, on average, a better financial investment than purchasing one in a non-college town (when comparing U.S. cities with populations less than 250,000 in 2010). Both at a monthly and yearly level, the sale prices of homes in college towns see better returns than those in non-college towns. Overall, college towns see higher increases in prices when the market as a whole sees price increases, and they see smaller decreases in the years when the market sees devaluations in home sale prices.

Although this trend holds for 19 of the 24 years included in the data set, only the months since 2004 have had a large enough sample size to reach 95% percent confidence that the difference between the two groups (college and non-college towns) could not have been the result of chance (p-value < 0.05).

In the course of the last 16 years (since 2004), mean home prices have risen during 10 of these years. In these ten years, prices in college towns rose an average of 1.12% more than those of non-college towns. In the last 16 years, mean home prices have fallen during 6 of those years. In these six years, prices in college towns fell an average of 1.69% less than those in non-college towns.

Examining the months since 2004, we see that home sales in college towns had more positive monthly price changes than did non-college towns in 115 out of 200 months. Pulling back to a yearly level, we find that since 2004 college towns have had more positive returns in 9 out of 16 years. During these years, their mean increase in home sale prices has been 2.53%, only 0.1% higher than in non-college towns.

Performing a t-test on these differences reveals that neither is significant enough to rule out the probability that the difference is the result of randomness (p-value for monthly changes is 0.74, while for yearly changes, it is 0.95).

It appears as though the considerably higher inflation in home sale prices in college towns over the last twenty-four years, as compared to non-college towns, is the combined result of consistently higher returns in the early recorded years, higher base prices, and the effects of compound returns.

The effect of COVID on home prices in college towns

Having been conducted during the 2020 COVID-19 pandemic, this study had to consider the following question: How has the pandemic affected housing prices in college towns?

Two new external factors are affecting pandemic pricing at the moment: one, an exodus from larger cities, and, two, the move of a large number of colleges to virtual classes.

With the recent general shift to remote-employment, many are realizing that they can work virtually anywhere. And so, many workers are moving to smaller cities—to cities within the size-range of our study. This migration has caused an increase in small city home prices.

At the same time that remote workers are moving to the At the same time that remote workers are moving to the country, students are doing the opposite. With many colleges allowing remote-attendance, fewer students are moving to college towns for the school year. In light of the reduced physical presence of students on their campuses, colleges are generating less revenue, and less external capital is being injected into the local economy. Furthermore, with fewer students living in college towns, there is less demand for apartments. This trend should drive rental prices down, and, in turn, lower home sale prices.

Given all the above, how are college towns fairing? In the past thirteen months, the average price of homes in cities with fewer than 250,000 inhabitants has gone up by 9.83% (0.76%/month mean). During this time, on average, home sale prices went up by 0.04% per month more in college towns than in non-college towns.

Statistically significant or not, college towns do tend to perform better than non-college towns, and the year 2020, despite the disruptions that COVID has caused to college life, has proved no exception.

Population size versus the presence of a college in a city as a predictor of home prices

Out of the U.S. cities with a population smaller than 250,000, college towns tend to have larger populations than do non-college towns. Within this group, non-college towns have a mean population size of 5936, while college towns have a mean population of 55,661, that is, larger by 49,725 people.

It is important then to determine if population size has a strong coefficient with home prices and change in home prices, since that could be the underlying cause of any difference between the two groups. It turns out, however, that population size is a very poor predictor of home prices.

Although there is a positive correlation between population size and home prices, the r-squared value is very weak (0.03 in 2010, and 0.04 in 2019). It's also worth noting that population increase correlates to home prices being higher in non-college towns than in college towns. Looking at the slope of the coefficient for college towns in both sampled years (2010 and 2019) the slope is nearly flat (0.0002 and 0.0003), whereas in both years, non-college towns had coefficients nearly five times larger (2.09 and 3.46). That the difference in these groups is caused by chance can confidently be rejected with p-values being well below 0.001 for both years.

A similar study examined population as a predictor of change in home sale prices (rather than raw home prices). This time, rather than examining two static points in time, two five year periods were examined, one from 2008-2013 when the overall housing market saw large declines, and the other from 2013-2018, when the housing market saw consistent positive growth.

Here we see an interesting effect. Population size correlates to significantly larger percentage increases in home sale prices in non-college towns than in college towns during the period when the market went up on a whole. But, during the years when the market went down, population correlated to equally larger declines in home value percentages lost over that period. It appears as though population size may correlate more strongly to volatility in home prices in non-college towns than in college towns. As before, we can reject the differences between college towns and non-college towns being arbitrary, as the p-value was well below 0.05 for both periods.

Population size turns out to be a weak predictor of home sale prices overall (r-squared values of 0.03 and 0.04 in the two sample years examined). Likewise, population size is a poor predictor of changes in home sale prices over two periods examined (one negative growth period with an r-squared value of 0.04 and one negative growth period with an r-squared value of 0.05). Despite these weak relationships between population size and home prices, my initial hypothesis that the presence of a college town is a stronger predictor of a higher increase in home values than is the population size turns out to be false.

The r-squared values for the relationships between the presence of a college in a city and both home sale prices, and changes in home sale prices, turn out to be very weak. Looking at home prices for 2010 and 2019, despite the college town mean being 44697 and 58398 higher respectively, the r-squared value for these differences was below 0.01.

The same held for the examination of changes in home sale prices in 2008-2013 and 2013-2018, the r-squared value for differences in these periods being below 0.01.

print("difference between CT and non-CT (% mean): {:.2f}".format( (monthly_data['ct_prcnt'] - monthly_data['nct_prcnt']).mean() ) )
print("return percent mean: {:.2f}".format( monthly_summary_data['returns_prcnt'].mean() ) )
print("standard deviation in return percent: {:.2f}".format( monthly_summary_data['returns_prcnt_std'].mean() ) )
print("return mean in positive months: {:.2f}".format( monthly_summary_data.loc[ (monthly_summary_data['returns_prcnt'] > 0) ]['returns_prcnt'].mean() ) )
print("return std in positive months: {:.2f}".format( monthly_summary_data.loc[ (monthly_summary_data['returns_prcnt'] > 0) ]['returns_prcnt_std'].mean() ) )
print("return mean in negative months: {:.2f}".format( monthly_summary_data.loc[ (monthly_summary_data['returns_prcnt'] < 0) ]['returns_prcnt'].mean() ) )
print("return std in negative months: {:.2f}".format( monthly_summary_data.loc[ (monthly_summary_data['returns_prcnt'] < 0) ]['returns_prcnt_std'].mean() ) )

difference between CT and non-CT (% mean): 0.08
return percent mean: 0.27
standard deviation in return percent: 0.81
return mean in positive months: 0.41
return std in positive months: 0.80
return mean in negative months: -0.29
return std in negative months: 0.83

Limitations

The average monthly change in home sale prices is +0.26%, with college towns seeing a 0.09% larger monthly average increase than non-college towns. Within each monthly change value, however, there is a 0.62% standard deviation. While the difference between college and non-college town returns is statistically significant for any given month, there are not enough months in the study for statistical significance across long time-periods.

Further analysis might include additional variables in predicting home sale prices, such as the cities' states.

Source code

The full source code used in this project is available on Github: https://github.com/szuc/info2950_project. This includes all pre-processing of data and third-party datasets.

Acknowledgments

In the course of this project, an incredibly large amount of time was spent looking through the Matplotlib pyplot documentation (which can be either interpreted as praise, or criticism of the documentation). Acknowledgments must also be given to a tutorial on Earth Lab that pointed me in the right direction on how to format dates in pyplot axes. Finally, StackOverflow deserves eternal acknowledgment for answering all my random syntax questions.

Appendix - Datasets: Sources and cleanup